by Fred Harwood
at the BCAMT Fall Conference-Gladstone, 10/21/16 Twitter: @HarMath Email: fharwood@sfu.ca and website: https://harmath.wordpress.com/
[Red Text throughout this blog are teacher moments that give context to why the workshop is designed as it is. Teaching is like juggling, as you become more adept, you add new objects to juggle, increase the difficulties and applications. Every one is at a different point in their teaching growth so, as you experience various structures in this workshop, which ones feel right to you to explore with your own students? On these first two pages, I provide the means to research them further with links to people who have been doing this well. You can also contact me for more information or if you have questions about any of these ideas.]
For you to embrace “Math Is Social”, you need to think about how students learn. I believe that learning has both acquisition and participatory aspects. You can be told, shown and discover ‘things’ but much of my greatest learning has occurred in participatory ‘social’ situations with a partner, group or class of individuals working together. Investigating a topic or problem collectively, we bounced ideas off of each other, challenged ideas or we were challenged by someone else’s idea. During the process, the talking and writing clarified our thinking, crystalized our learning and extended our investigations. Achieving success after productive struggles, encountering AHA moments, eliciting peer commendations all built motivation and belief in our abilities to solve other problems and to acquire good dispositions for thinking. I wish for all of you to have these moments and successes.
This workshop will focus on some structures that will support building collaboration, communication, reasoning and understanding socially. If you haven’t learned of a Thinking Classroom from Professor Peter Liljedahl, check out: http://peterliljedahl.com/wp-content/uploads/Building-Thinking-Classrooms-Feb-14-20151.pdf
We want our students to think, to solve problems and to be able to communicate their solutions (processes and not just answers). The following structures are some of the ways that facilitate these qualities. Some may be already part of your teaching practices and others may be new. Remember, as much as possible, to observe the learning and emotions taking place in yourselves and others while engaging in these structures. Switch your student hat with your teacher hat and researcher hat frequently.
Structures of a socially dynamic classroom include:
http://mathsolutions.com/common-core-support/math-talk/resources/#MathTalk-1
- Fraction Talks: http://fractiontalks.com and http://www.fractiontalks.com/p/how-to.html
- Visual Patterning: http://www.visualpatterns.org/ and http://www.visualpatterns.org/teachers.html
- Chunked Families of Questions: clustering questions in groups with variance for students to seek patterns, connections and to discuss these.
- Partnered Games: Taking games, like Ultimate TicTacToe or Mancala, and having students play with a partner against another pair creates reasoning aloud in strategy planning, game observations and pattern recognition.
- Good Problems: Rich problems with multiple approaches and good math content lead to students being engaged in the challenge of solving them especially through discussion. Do not fail to realize that you and your students can create your own good problems. They can also be found. Some of my favourite sources are: http://www.peterliljedahl.com/teachers/numeracy-tasks http://www.peterliljedahl.com/teachers/good-problem http://www.peterliljedahl.com/teachers/good-problem http://nrich.maths.org/ http://illuminations.nctm.org/ and a myriad of great links through #MTBoS like http://www.estimation180.com/ http://wmh3acts.weebly.com/3-act-math.html https://tapintoteenminds.com/3act-math/ and the portal site: https://thelearningkaleidoscope.wordpress.com/resources/
Many great problems also emerge from extensions on any of the problems you might start with. These emergent inquiries are a rich source.
Keep in mind in your planning and execution these dimensions from http://map.mathshell.org/trumath/trumath_dimensions_alpha.pdf

[These first two pages are background information and links to pursue any of the ideas the participants find the most intriguing further. I strongly suggest you experience being a student in doing the following activities with others. “Math is Social” so the workshop is designed to model what students would go through in these structures and to then be excited by the amount of mathematics learned, the positive dispositions gained, the lessening of math anxiety and the dynamic and motivating attitude to question further!]
Let us experience some of these structures . . . [groups actually worked through these and we utilized different approaches to structure the opportunities for students to talk, describe, justify, defend and challenge ideas mathematically.]
- Math Talks: [In this workshop I used this variation on Number/Math Talks: Give wait time to let students (teachers) think, try the problem on their own for a little while then they worked with a partner or two to add to their techniques. A team was asked to post on the wall one of their ways, then, with each new group, a new method needed to be posted creating an array of around 11 various approaches. The teacher now orchestrates the discussion by having various students explain their posting and then the teacher draws attention to various approaches with questions like: Which ones are similar and why? How is this one different? Which one(s) did you really like? Don’t just leave multiple representations up without students being forced to see more of the mathematics that is there.]
Figure out what 44 x 25 is in multiple ways. Be ready to show others around you how you did each method. You’ll have some think time by yourself and then I’d like you to pair up with someone nearby to share with each other.
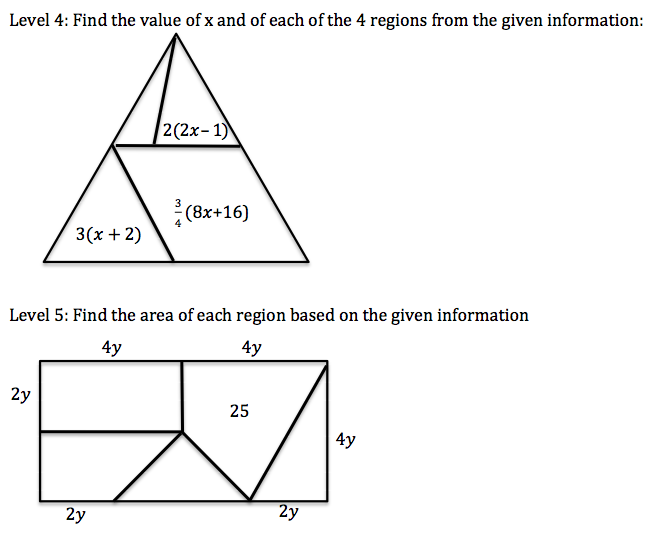
2. Fraction Talk: [A variation on Math Talks is Fraction Talks which draw proportional reasoning into their logic skill-set. Proportional Reasoning is one of the really BIG IDEAS in mathematics. I hinted that, after doing some of these with students, they could have solved Fawn’s problem of the missing yellow region’s area very quickly.]
What fraction of the whole is each region in each of the following diagrams?

Fraction Talk Extensions: [These extensions were an attempt to draw older students into algebraic thinking with clotheslines (rulers) and fraction talks with unknowns but proportionally related.]

4. IMAGINE EDUCATION: Our goal today is to ‘see’ mathematics and to see it talk to us. You will need to imagine how other students are thinking and ‘show’ what they might have done to count how many dots are in an array: [I think I will add some with words instead of arithmetic expressions like #2 which could be “I saw two sixes but missing two corners.”]

[What mathematics would employed in the following inquiry? What other curricular areas would also be addressed like descriptive writing in the activity? What ownership could be shared if students were allowed to use their camera phones to explore from a ‘lowered or raised perspective’? How much imagination is employed?]

5. Visual Patterning: [Visual patterning in growing patterns is a fantastic way to engage students in mathematical thinking, patterning, generalizing, verifying, and much more high quality mathematics. I used stars in these ones so I could have flip chip manipulatives available for participants to make their pattern’s growth obvious and to defend their generalizations. I found my teacher/students had 3 different working formulae for each of the patterns which led to a good discussion on equivalent expressions and on ‘seeing’ how each could be represented in the chips powerfully.]
1.) Work with partners to solve this growing pattern’s questions. Remember you are trying to ‘show’ how you thought through the problem clearly enough for others to understand your method and the process you did to solve the problems.

- What would Figure 4 look like?
- How many stars in Figure 8?
- How many stars in Figure 12
- Can you generalize a formula or formulae to predict the number of stars in any Figure?
- If there was a Figure 0, what would it look like and why?
Bonus Pattern: Answer the same questions as above:

5. Chunked Families of Questions: Figure out each and connect them with a larger pattern of understanding. Create your own algorithm. Can they all be done in your head after you’ve discovered the larger pattern? [By working out the answers but knowing someone can do all of them in their heads faster than they could be entered in a calculator engages the students to connect questions with answers, questions with questions and to discover larger patterns of understanding. Visual patterns did the same thing in connecting Figure Numbers with their shapes to generalize a more powerful pattern. These families of problems also provoke students to ask their own questions to pursue the inquiry further. The movement of ‘nixing the tricks’ and ‘banning the worksheets’ misses how much mathematics can be uncovered/learned in well designed sheets which draw students into inquiry (much like a science lab does). These create life skills, attitudes and dispositions that will lead to much success.]

6. Partnered Games: playing a variety of games especially as two against two to create the structure for math talk with each other (also called strategy, strategic planning, observing the enemy, seeking patterns . . . ) [100 minutes left us just mentioning these last two sections but these are very powerful as structures for mathematical discussions while being engaged in the activities.]
Example:
Ultimate Tic Tac Toe
Rules can be found here:
http://mathwithbaddrawings.com/2013/06/16/ultimate-tic-tac-toe/
Online version: http://ultimatetictactoe.creativitygames.net/

7. Good Problems: These are single problems that are challenging enough to make students want to persevere in solving them but need to do lots of talk with their groups to get to their understanding of the problem to solve it.
from http://www.peterliljedahl.com/teachers/good-problem
Square Peg in a Round Hole
What is a better fit, a square peg in a round hole or a round peg in a square hole?
Chessboard
How many squares on a weird 6x 10 chessboard? How many rectangles?

I like the juggling metaphor for teaching. I taught my best Math lesson in a long time today; it had a lot of moving pieces yet it happened quite ‘off the cuff.’ I was motivated to give context to teaching place value so I had to come up with a believable story involving my students. One thing I really value from your mentorship is learning to ask a sequence of questions that leads to learning rather than ‘telling.’ It is not easy but it is so valuable.
LikeLike